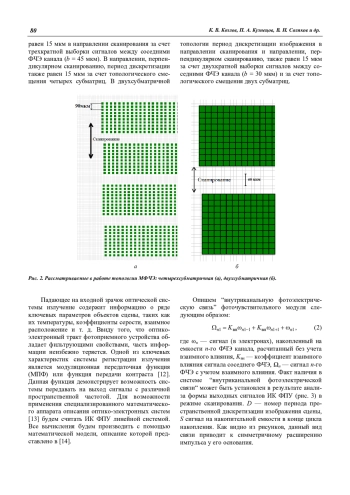
Проведено комплексное теоретическое исследование, позволившее оценить степень влияния взаимосвязи сигналов многорядного крупноформатного фотоприемного устройства (ФПУ) на его характеристики. Предложено классифицировать виды взаимосвязи следующим образом, а именно, выделить два вида фотоэлектрической связи: “внутриканальную фотоэлектрическую связь” и “межканальную фотоэлектрическую связь”, а также два вида электрической связи: “взаимосвязь в схеме ВЗН-суммирования” (ВЗН — временная задержка и накопление) и “взаимосвязь внутри блока сопряжения”. Представлены формы выходных сигналов ФПУ, характерные для каждого вида взаимосвязи сигналов. Вычисления проведены для двух различных топологий матриц фоточувствительных элементов. Результаты, полученные в работе, применимы для широкого класса инфракрасных (ИК) ФПУ с режимом ВЗН.
A complex theoretical research of the TDI FPA signals correlation has been done. The classification of correlation types is showed. According to this classification, there are two types of photoelectrical classification: “in channel correlation” and “between channels correlation” and two types of electrical classification: “TDI correlation” and “preamplifier correlation”. The TDI output characteristics with correlation have been obtained. The calculations are implemented for two types of photosensitive elements topologies. The results are acceptable for a wide range of TDI FPA.
Идентификаторы и классификаторы
- SCI
- Физика
- eLIBRARY ID
- 25480318
Предложена классификация видов взаимосвязи многорядного ИК ФПУ, включающая в себя два вида фотоэлектрической связи: “внутриканальную фотоэлектрическую связь” и “межканальную фотоэлектрическую связь”, а также два вида электрической связи: “взаимосвязь в схеме ВЗНсуммирования” и “взаимосвязь внутри блока сопряжения”.
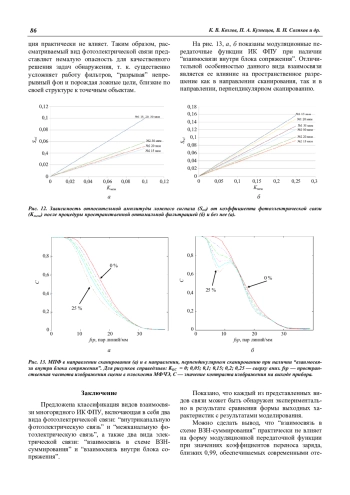
Показано, что каждый из представленных видов связи может быть обнаружен экспериментально в результате сравнения формы выходных характеристик с результатами моделирования.
Можно сделать вывод, что “взаимосвязь в схеме ВЗН-суммирования” практически не влияет на форму модуляционной передаточной функции при значениях коэффициентов переноса заряда, близких 0,99, обеспечиваемых современными отечественными технологическими процессами. Как показали результаты исследований, опубликованные в работе [15], амплитуда сигнала от малоразмерного объекта при этом понижается менее, чем на 10 % для четырехсубматричной топологии. Таким образом, не имеет смысла уменьшать расстояние между соседними ФЧЭ канала, увеличивая при этом риск повышения “внутриканальной фотоэлектрической связи”.
Показано, что взаимосвязь внутри блока сопряжения представляет немалую опасность для качественного решения задач обнаружения, т. к. существенно усложняет работу фильтров, “разрывая” непрерывный фон и порождая ложные цели, близкие по своей структуре к точечным объектам. Улучшение отношения сигнал/помеха в результате оптимальной фильтрации при диаметре точечной цели, равном 30 мкм, и значении коэффициента взаимного влияния, равном 10 %, составляет ≈30 %, так что использование фильтрации все равно оправдано по отношению к помехам данного вида. Большая часть других видов связи, вызванных близким расположением электрических шин, утечками емкостей и т. д. с точки зрения математического описания могут быть сведены к “взаимосвязи внутри блока сопряжения” путем задания соответствующего алгоритма коммутации сигналов, так что полученные результаты обладают достаточной общностью.
Список литературы
1. Козлов К. В., Соляков В. Н., Кузнецов П. А., Полесский А. В., Хамидуллин К. А., Семенченко Н. А., Бедарева Е. А. // Успехи прикладной физики. 2014. Т. 2. № 4. С. 55.
2. Тришенков М. А. Фотоприемные устройства и ПЗС. Обнаружение слабых оптических сигналов. — М.: Радио и связь, 1992.
3. Филачев А. М., Таубкин И. И., Тришенков М. А. Твердотельная фотоэлектроника. Физические основы. — М.: Физматкнига, 2005. — 384 с.
4. Александров В. В., Бычковский Я. С., Дражников Б. Н., Козлов К. В., Кондюшин И. С., Матвеев А. В. // Прикладная физика. 2014. № 6. C. 81.
5. Козлов К. В., Бычковский Я. С., Кондюшин И. С., Матвеев А. В., Соляков В. Н., Пожидаев Д. А., Балиев Д. Л. // Успехи прикладной физики. 2014. Т. 2. № 2. C. 170.
6. Филачев А. М., Бурлаков И. Д., Болтарь К. О., Дражников Б. Н., Хромов С. С., Кузнецов П. А. / Труды 22-й Международной научно-технической конференция по фотоэлектронике и приборам ночного видения, 22—25 мая 2012 г., Москва, ФГУП «НПО «Орион». C. 22—24.
7. Бочков В. Д., Дражников Б. Н., Кузнецов П. А., Козлов К. В., Соляков В. Н. // Прикладная физика. 2014. № 1. С. 58.
8. Кузнецов П. А., Мощев И. С., Хромов С. С. // Успехи прикладной физики. 2013. Т. 1. № 5. С. 606.
9. Кузнецов П. А., Мощев И. С. // Успехи прикладной физики. 2015. Т. 3. № 1. С. 71.
10. Кузнецов П. А. Хромов С. С., Зайцев А. А. // Прикладная физика. 2012. № 5. С. 95.
11. Демидов В. И., Колесова А. А., Полесский А. В., Смирнова Е. А., Хамидуллин К. А. // Успехи прикладной физики. 2013. Т. 1. № 5. С. 625.
12. Ллойд Дж. Системы тепловидения. — М.: Мир, 1978.
13. Госсорг Ж. Инфракрасная термография. Основы, техника, применение. Пер. с франц. — М.: Мир, 1988.
14. Васильев В. Н., Дмитриев И. Ю., Дражников Б. Н., Козлов К. В., Кузнецов П. А., Соляков В. Н., Пономаренко В. П. // Успехи прикладной физики. 2015. Т. 3. № 5. С. 486.
15. Козлов К. В., Кузнецов П. А. // Прикладная физика. 2015. № 3. С. 61.
16. Дражников Б. Н., Козлов К. В., Кузнецов П. А., Соляков В. Н. // Успехи прикладной физики. 2015. Т. 3. № 6. С. 566.
1. K. V. Kozlov, V. N. Solyakov, P. A. Kuznetsov, A. V. Polesskii, K. A. Khamidullin, N. A. Semenchenko, and E. A. Bedareva, Uspekhi Prikladnoi Fiziki 2, 55 (2014).
2. M. A. Trishenkov, Photoreceiver Devices and CCD. (Radio Svyaz’, 1992) [in Russian].
3. A. M. Filachev, I. I. Taubkin, and M. A. Trishenkov, Solid State Photoelectronics. Physical Principles (Fizmatkniga, Moscow, 2005) [in Russian].
4. V. V. Aleksandov, Ya. S. Bychkovskii, B. N. Drazhnikov, K. V. Kozlov, I. S. Kondyushin, and A. V. Matveev, Prikladnaya Fizika, No. 6, 81 (2014).
5. K. V. Kozlov, Ya. S. Bychkovskii, I. S. Kondyushin, A. V. Matveev, V. N. Solyakov, D. A. Pozhidaev, and D. L. Baliev, Uspekhi Prikladnoi Fiziki 2, 170 (2014).
6. A. M. Filachev, I. D. Burlakov, K. O. Boltar, B. N. Drazhnikov, S. S. Khromov, and P. A. Kuznetsov, in Proc. XXII Intern. Conf. Photoelectronics, May 22–25, 2012 (NPO Orion, Moscow) P. 22—24.
7. V. D. Bochkov, B. N. Drazhnikov, P. A. Kuznetsov, K. V. Kozlov, and V. N. Solyakov, Prikladnaya Fizika, No. 1, 58 (2014).
8. P. A. Kuznetsov, I. S. Moshchev, S. S. Khromov, Uspekhi Prikladnoi Fiziki 1, 606 (2013).
9. P. A. Kuznetsov and I. S. Moshchev, Uspekhi Prikladnoi Fiziki 3, 71 (2015).
10. P. A. Kuznetsov, S. S. Khromov, and A. A. Zaitsev, Prikladnaya Fizika, No. 5, 95 (2012).
11. V. I. Demidov, A. A. Kolesova, A. V. Polesskii, E. A. Smirnova, and K. A. Khamidullin, Uspekhi Prikladnoi Fiziki 1, 625 (2013).
12. J. Lloid, Systems of Thermovision (Mir, Moscow, 1978) [in Russian].
13. J. Gossorg, Infrared Thermograph (Mir, Moscow, 1988) [in Russian].
14. V. N. Vasil’ev, I. Yu. Dmitriev, B. N. Drazhnikov, K. V. Kozlov, P. A. Kuznetsov, V. N. Solyakov, and V. P. Ponomarenko, Uspekhi Prikladnoi Fiziki 3, 486 (2015).
15. K. V. Kozlov and P. A. Kuznetsov, Prikladnaya Fizika, No. 3, 61 (2015).
16. B. N. Drazhnikov, K. V. Kozlov, P. A. Kuznetsov, and V. N. Solyakov, Uspekhi Prikladnoi Fiziki 3, 566 (2015).
Выпуск

С О Д Е Р Ж А Н И Е
ОБЩАЯ ФИЗИКА
Аверин И. А., Бердников А. С. Краевые поля бессеточных электронных спектрографов с однородными по Эйлеру электростатическими полями 5
Коберник Д. А., Никольский В. А., Руденко В. В. Возмущение низкочастотных электромагнитных полей в волноводе земля-ионосфера сферической неоднородностью, заглубленной под поверхностью земли 9
Наумов Н. Д. Оценка поля электромагнитного импульса в параксиальной области 19
Мелкумян Б. В. Определение газовых потоков активной среды лазерного гироскопа 24
Голофастова А. С., Новиковский Н. М., Разномазов В. М., Павленко А. В., Вербенко И. А., Сарычев Д. А., Резниченко Л. А., Махиборода А. В. Определение стехиометрического состава твердых растворов (1-x)BiFeO3–xPbFe1/2Nb1/2O3 методом рентгеновского флуоресцентного анализа с полным внешним отражением 32
Акаткин О. А., Кулиш О. А., Петрова О. В. Моделирование изодозных распределений в низкоатомной среде при облучении пучком нейтронов высоких энергий 37
ФИЗИКА ПЛАЗМЫ И ПЛАЗМЕННЫЕ МЕТОДЫ
Болдырев М. С., Наумов Н. Д., Никольский В. А., Урядов В. П. Модель рассеяния коротких радиоволн искусственными ионосферными неоднородностями 41
Долгов А. Н., Клячин Н. А., Прохорович Д. Е. Полоидальные структуры в плазме Z-пинча 46 ФОТОЭЛЕКТРОНИКА Бурлаков И. Д., Филачев А. М., Холоднов В. А. Аналитическое описание характеристик лавинных фо-тодиодов (обзор). Часть I 52
Козлов К. В., Кузнецов П. А., Соляков В. Н., Хамидуллин К. А., Антипов Н. С. Классификация и исследование взаимосвязи каналов крупноформатного многорядного инфракрасного фотоприемного устройства 78
ФИЗИЧЕСКАЯ АППАРАТУРА И ЕЁ ЭЛЕМЕНТЫ
Бердников А. С., Аверин И. А. Новый подход к разработке ионно-оптических схем статических масс-спектрографов на основе неоднородных магнитных полей, однородных по Эйлеру 89
ПЕРСОНАЛИИ
Юбилейная дата И. Д. Бурлакова 96
Вспоминая о Л. А. Бовиной 98
ИНФОРМАЦИЯ
24-я Международная научно-техническая конференция по фотоэлектронике и приборам ночного видения 100
Правила для авторов 103
Бланк для подписки 106
C O N T E N T S
GENERAL PHYSICS
I. A. Averin and A. S. Berdnikov Fringe fields of gridless electronic spectrographs with Euler’s homogeneous electrostatic fields 5
D. A. Kobernik, V. A. Nikolsky, and V. V. Rudenko The effect of the excitation of low-frequency electromagnetic fields in an earth-ionosphere waveguide by a sub-surface buried spherical inhomogeneity 9
N. D. Naumov Pulse field estimation for a paraxial region 19
B. V. Melkoumian Laser gyro active media gas flow determination 24
A. S. Golofastova, N. M. Novikovskiy, V. M. Raznomazov, A. V. Pavlenko, I. A. Verbenko, D. A. Sarychev, L. A. Reznichenko, and A. V. Makhiboroda Determination of stoichiometric composition of the solid solution (1-x)BiFeO3–xPbFe1/2Nb1/2O3 by TXRF analysis 32
O. A. Akatkin, O. A. Culish, and O. V. Petrova Modelling of an isodose distribution of irradiation with high energy neutrons beams in a low atomic number medium 37
PLASMA PHYSICS AND PLASMA METHODS
M. S. Boldyrev, N. D. Naumov, V. A. Nikolskiy, and V. P. Uryadov The technique for a specular scattering of short radio waves from artificial ionospheric irregularities 41
A. N. Dolgov, N. A. Klyachin, and D. E. Prokhorovich Poloidal structures of the Z-pinch plasma 46
PHOTOELECTRONICS
I. D. Burlakov, А. М. Filachev, and V. A. Kholodnov Analytical description of characteristics of the avalanche photodiodes (a review). Part I 52
K. V. Kozlov, P. A. Kyznetsov, V. N. Solyakov, K. A. Chamidullin, and N. S. Antypov The investigation of TDI FPA signals correlation 78
PHYSICAL EQUIPMENT AND ITS ELEMENTS
A. S. Berdnikov and I. A. Averin A new approach to development of ion-optical systems for static mass spectrographs on the basis of the non-uniform Euler’s homogeneous magnetic fields 89
PERSONALIA
Anniversary Date of I. D. Burlakov 96
Remembering about L. A. Bovina 98
INFORMATION
XXIV International Conference on Photoelectronics and Nigth Vision Devices 100
Rules for authors 103
Subscription to the Journal 106
Другие статьи выпуска
На фоне современных способов проведения масс-анализа статические масс-анализаторы иногда считаются безнадёжно устаревшими и пригодными для решения лишь узкоспецифичных задач. Однако новые технологические решения (в частности, использование сильных постоянных магнитов со сложными профилями наконечников, использование параллельных детекторов высокого пространственного разрешения типа микроканальных пластин и фотодиодных матриц, и т. п.) вполне способны придать новое дыхание этому направлению. В данной статье рассматриваются теоретические способы, как на основе неоднородных статических магнитных полей, однородных по Эйлеру, можно разрабатывать схемы статических масс-спектрографов нового типа. Важно, что указанные массспектрографы характеризуются большим диапазоном масс в спектре, обладают строго линейной линией фокусов и демонстрируют одинаково высокое качество фокусировки (а именно, двойную фокусировку второго порядка по углу, энергии и дополнительно по вертикальному смещению) в любой точке линии фокусов.
Представлены аналитические выражения для коэффициентов лавинного размножения носителей в p–n-структурах. Рассмотрены наиболее характерные ситуации: ступенчатый (резкий) и плавный (линейный) p–n-переходы и тонкая p+–n(p)–n+-структура (типа p–i–n). Выведены формулы для напряжения лавинного пробоя VBD и показателя степени в соотношении Миллера для зависимости коэффициента размножения носителей от приложенного напряжения V. На примере полупроводников Ge, Si, GAP и InSb показано, что полученные аналитические результаты находятся в хорошем количественном согласии с проведенными ранее численными расчетами и экспериментальными данными. Эти результаты позволяют быстро и с хорошей точностью оценивать коэффициенты размножения электронов и дырок при заданном приложенном напряжении V.
Проведен теоретический анализ зависимости межзонного туннельного тока гетероструктуры с p+–n-переходом в ″широкозонном″ слое от параметров используемых полупроводниковых материалов, уровней легирования ″высокоомных″ слоев и их толщин при напряжениях лавинного пробоя гетероструктуры. Показано, что туннельный ток, как правило, немонотонно зависит от концентрации легирующей примеси в ″высокоомной″ части ″широкозонного″ слоя. В наиболее практически интересном случае существует оптимальная концентрация этой примеси, при которой для заданных толщин слоев и уровня легирования ″узкозонного″ слоя туннельный ток достигает абсолютного минимума. Выведена простая формула для определения величины этой концентрации. Получено также аналитическое выражение для определения минимального значения туннельного тока. В реальных случаях перепад токов может составлять несколько порядков. Выяснено, что увеличение уровня легирования ″узкозонного″ слоя во многих случаях приводит к уменьшению туннельного тока. Показано, что при понижении уровня легирования ″высокомных″ слоев гетероструктуры туннельный ток не обращается в нуль, а начиная с некоторой концентрации перестает зависеть от уровня легирования. Аналогичный эффект имеет место и для гомогенного p+–n-перехода. Обсуждаются физические причины такого поведения туннельного тока при напряжениях лавинного пробоя. Разработана методика оптимизации параметров гетероструктуры порогового лавинного фотодиода с разделенными областями поглощения и умножения. Проведены конкретные расчеты, например, для широко используемой системы InP-In0,53Ga0,47As-InP.
Рассмотрена возможность описания переходных процессов в p–i–n лавинных фотодиодах (ЛФД) элементарными функциями, прежде всего, при начальном напряжении V0, большем напряжения лавинного пробоя VBD. Постановка задачи вызвана потребностью знать явные условия возникновения гейгеровской моды работы ЛФД. Выведено несложное выражение, описывающее динамику лавинного гейгеровского процесса. Получена формула для полного времени его протекания. Представлено явное аналитическое соотношение реализации моды Гейгера. Определены условия применимости полученных результатов.
В заключение на основе аналитических вычислений обсуждены и продемонстрированы преимущества лавинных гетерофотодиодов (ЛГФД) с разделенными областями поглощения и умножения (РОПУ) типа ‘‘low-high-low’’ перед классическими образцами.
Проведено исследование пространственной структуры и динамики плазмы в разряде сильноточной вакуумной искры методом импульсной тенеграфии. Зарегистрировано формирование полоидальных структур в плазме перетяжки на стадии завершения процесса пинчевания.
Предполагается использовать импульс мягкого рентгеновского излучения для воздействия на мишень, содержащую термоядерное топливо, для ее сжигания и нагрева. Подобные устройства оказываются пригодными для инновационного решения ряда прикладных задач.
В работе представлена модель расчёта геометрии ракурсных контуров на земной поверхности, характеризующих рассеяние коротких радиоволн передатчика мелкомасштабными магнитно-ориентированными неоднородностями электронной концентрации, искусственно созданных в верхней ионосфере в результате работы нагревного стенда. Модель основана на решении системы дифференциальных уравнений, описывающих лучевую траекторию распространения радиоволны в трёхмерно-неоднородной ионосфере. Проведено сравнение результатов, полученных расчётным путём при использовании разработанной модели, с данными, полученными в результате экспериментальных исследований по ракурсному рассеянию декаметровых радиоволн с линейной частотной модуляцией, проведённых на отечественном стационарном среднеширотном нагревном стенде Сура в период 09-14 сентября 2013 г.
Разработана модель для прогноза поглощенных доз в низкоатомной среде при облучении нейтронами высоких энергий. Она основана на обыкновенных дифференциальных уравнениях первого порядка. Их решениями аппроксимированы распределения этих доз в объеме среды. Параметры решений определены по данным измерений. По этим распределениям рассчитаны изодозные карты. На их основе спрогнозированы соответствующие распределения доз. При этом трудоемкая задача расчета и визуализации изодозных распределений сведена к численному решению системы алгебраических уравнений. Для заданных условий результаты моделирования сравнены с результатами измерений. Они хорошо совпадают. Модель найдет применение в радиационной физике и дозиметрии нейтронного излучения.
В работе показана возможность определения стехиометрического состава твердых растворов (1-x)BiFeO3–xPbFe1/2Nb1/2O3 методом рентгенофлуоресцентного анализа на спектрометре РФС-001 с полным внешним отражением рентгеновского излучения (TXRF). Исследовался элементный состав 15 образцов керамики с изменением стехиометрического коэффициента x в диапазоне значений от 0,25 до 0,95. Исследуемая проба представляла из себя мелкодисперсный порошок массой порядка нескольких мг. Описаны ключевые этапы синтеза твердых растворов (1-x)BiFeO3–xPbFe1/2Nb1/2O3. Перечислены основные характеристики TXRF спектрометра РФС-001. Описана подготовка проб к анализу и методика определения стехиометрического коэффициента x на TXRF- спектрометре. Приводится формула расчета стехиометрического коэффициента x по экспериментальным данным значений интенсивностей L-серий рентгеновской флуоресценции висмута и свинца. Проведено сопоставление экспериментально полученных методом рентгенофлуоресцентного анализа коэффициентов х с их значениями, закладываемыми при синтезе твердых растворов. Показано, что метод рентгенофлуоресцентного анализа на TXRF-спектрометре позволяет с высокой точностью контролировать элементный состав, определяющий уникальные электрофизические, магнитные и магнитодиэлектрические свойства высокотемпературных мультиферроиков. Данная методика позволяет уйти от сложной пробоподготовки, необходимой при традиционном рентгеновском флуоресцентном анализе, что уменьшает время анализа и удешевляет процесс контроля качества синтезируемых материалов.
Предложен метод неразрушающего контроля газовых потоков активной среды кольцевого лазера, обусловленных неоднородным тепловым полем в кольцевом резонаторе. Скорость потока определяется через измеряемые величины: эффективную частоту возбуждения электрическим полем, эффективную частоту теплового ухода возбуждённых атомов на стенки разрядной трубки, температуру внешней стенки активной среды и среднюю температуру в корпусе кольцевого лазера. Предлагаемая физическая модель нагрева среды позволяет повысить точность лазерного гироскопа.
Рассматривается задача о распространении в диспергирующей и поглощающей среде импульса, формируемого с помощью параболического рефлектора. Для описания пространственно-временной эволюции импульса используется метод параболического уравнения. Разработанный метод позволяет оценить для ближней и дальней зоны поле импульса в параксиальной области с учетом влияния эффекта дифракции и свойств среды. Получено аналитическое выражение для поля импульса на оси рефлектора. Показано, что для электромагнитного импульса в вакууме это выражение согласуется с известным результатом, что во временной области сигнал в зоне Фраунгофера соответствует производной исходного импульса. Проанализировано влияние поглощения на искажение акустического импульса. Рассмотрена модельная задача о компрессии электромагнитного импульса в холодной плазме без столкновений.
В трехмерной постановке разработана модель для описания распространении низкочастотного излучения в волноводе земля-ионосфера. Построена аналитическая модель. Получены закономерности для электромагнитных полей от расположенного в волноводе или в нижней ионосфере СНЧ-источника. Рассматриваются поля в волноводе, ионосфере и подстилающей поверхности земли. Под поверхностью земли решается задача о рассеянии этого излучения на заглубленной сферической неоднородности. Получены аналитические оценки для пустотной и неоднородности с высокой проводимостью. Для рассеянного излучения исследована структура электромагнитного поля над поверхностью земли. Получено сопоставление начального и рассеянного полей в волноводе в зависимости от исходных характеристик СНЧ-источника, глубины залегания и электромагнитных свойств неоднородности и земли. Результаты расчетов сопоставлены с уровнем естественных шумов в волноводе. Сделаны выводы о возможности зондирования слабо заглубленных объектов. Полученный уровень возмущения начального поля оказывается относительно слабым для проведения аэроразведки, но оставляет возможности для идентификации заглубленного объекта с поверхности земли.
Предметом исследования являются краевые поля электронных спектрографов с однородными по Эйлеру электрическими полями. Большинство рассмотренных ранее оптических схем используют приближение идеального скачка электрического поля для краевой области, что на практике приводит к дополнительным краевым полям, разрушающим идеальные спектрографические свойства исходной оптической схемы. В данной работе показано, как можно организовывать строго однородные по Эйлеру трёхмерные электростатические поля, которые сохранят идеальные спектрографические свойства и обеспечат бессеточный ввод и вывод частиц.
Статистика статьи
Статистика просмотров за 2026 год.
Издательство
- Издательство
- АО "НПО "ОРИОН"
- Регион
- Россия, Москва
- Почтовый адрес
- 111538, г Москва, р-н Вешняки, ул Косинская, д 9
- Юр. адрес
- 111538, г Москва, р-н Вешняки, ул Косинская, д 9
- ФИО
- Старцев Вадим Валерьевич (ГЕНЕРАЛЬНЫЙ ДИРЕКТОР)
- E-mail адрес
- orion@orion-ir.ru
- Контактный телефон
- +7 (499) 3749400