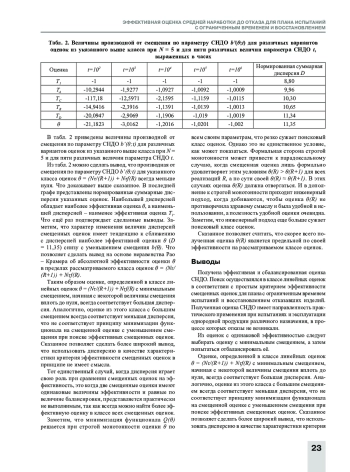
В качестве показателя, характеризующего такое свойство надежности сложного восстанавливаемого изделия, как безотказность, выбирают в соответствии со средней наработкой до отказа (далее – t). С организационной и экономической точек зрения наиболее подходящим для испытаний восстанавливаемых (заменяемых) изделий при условии подчинения наработки до отказа экспоненциальному закону распределения вероятностей является план NBτ, где N – число испытуемых однотипных изделий; τ – наработка (одинаковая для каждого изделия); B – характеристика плана, означающая, что работоспособность изделия после каждого отказа в течение срока испытаний восстанавливается. Традиционно в качестве оценки средней наработки до отказа (СНДО) выбирается оценка t1 = Nτ/R, где R > 0 – количество наблюдаемых отказов, которые произошли в течение времени τ. Эта оценка является смещенной и, кроме того, если за время испытаний наблюдается небольшое число отказов (порядка нескольких единиц) или не наблюдается, то эта оценка может дать значительную ошибку из-за смещения. За последнее время появились оценки СНДО лишенные указанных недостатков. Однако эти полученные оценки не являются абсолютно эффективными.
Цель работы. Целью работы является построение более эффективной оценки СНДО для плана испытаний с ограниченным временем и восстановлением.
Методы. При сравнении оценок СНДО на эффективность используется простой критерий эффективности смещённых оценок.
Выводы. 1. Получена эффективная и сбалансированная оценка СНДО. Поиск осуществлялся в классе линейных оценок в соответствии с простым критерием эффективности смещенных оценок для плана с ограниченным временем испытаний и восстановлением отказавших изделий. Полученная оценка СНДО имеет направленность практического применения при испытаниях и эксплуатации однородной продукции различного назначения, в процессе которых отказы не возникали;
2. Из оценок с одинаковой эффективностью следует выбирать оценку с минимальным смещением, а затем попытаться отбалансировать её.
3. Оценке, определенной в классе оценок θ = (Nτ/(R+1)) + Nτf(R) с минимальным смещением, начиная с некоторой величины смещения вплоть до нуля, всегда соответствует большая дисперсия. Аналогично, оценке из этого класса с большим смещением всегда соответствует меньшая дисперсия, что не соответствует принципу минимизации функционала на смещенной оценке с уменьшением смещения при поиске эффективных смещенных оценок. Сказанное позволяет сделать более широкий вывод, что использовать дисперсию в качестве характеристики критерия эффективности смещенных оценок в принципе не имеет смысла.
Предпросмотр статьи
Идентификаторы и классификаторы
- Префикс DOI
- 10.21683/1729-2646-2025-25-2-19-24