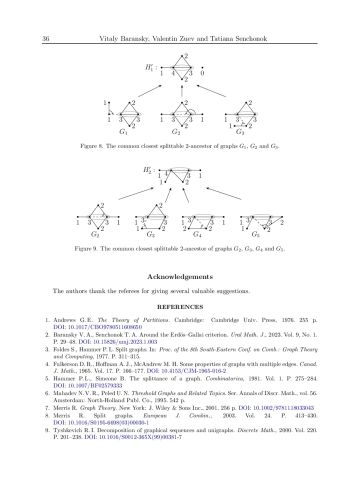
A graph G is splittable if its set of vertices can be represented as the union of a clique and a coclique. We will call a graph H a {splittable ancestor} of a graph G if the graph G is reducible to the graph H using some sequential lifting rotations of edges and H is a splittable graph. A splittable r-ancestor of G we will call its splittable ancestor whose Durfey rank is r. Let us set s=(1/2)(sumtl(λ)−sumhd(λ)), where hd(λ) and tl(λ) are the head and the tail of a partition λ. The main goal of this work is to prove that any graph G of Durfey rank r is reducible by s successive lifting rotations of edges to a splittable r-ancestor H and s is the smallest non-negative integer with this property. Note that the degree partition dpt(G) of the graph G can be obtained from the degree partition dpt(H) of the splittable r-ancestor H using a sequence of s elementary transformations of the first type. The obtained results provide new opportunities for investigating the set of all realizations of a given graphical partition using splittable graphs.
Идентификаторы и классификаторы
- УДК
- 51. Математика
Everywhere we mean by a graph a simple graph, i. e., a graph without any loops and multiple edges. We will adhere to the terminology and notation from [1, 2, 6].
An integer partition, or simply, a partition is a non-increasing sequence λ = (λ1, λ2,…) of non-negative integers that contains only a finite number of non-zero components (see [1]).
Список литературы
1. Andrews G. E. The Theory of Partitions. Cambridge: Cambridge Univ. Press, 1976. 255 p. DOI: 10.1017/CBO9780511608650
2. Baransky V. A., Senchonok T. A. Around the Erdös-Gallai criterion. Ural Math. J., 2023. Vol. 9, No. 1. P. 29-48. DOI: 10.15826/umj.2023.1.003 EDN: RKQOHI
3. Foldes S., Hammer P. L. Split graphs. In: Proc. of the 8th South-Eastern Conf. on Comb.: Graph Theory and Computing, 1977. P. 311-315.
4. Fulkerson D. R., Hoffman A. J., McAndrew M. H. Some properties of graphs with multiple edges. Canad. J. Math., 1965. Vol. 17. P. 166-177. DOI: 10.4153/CJM-1965-016-2
5. Hammer P. L., Simeone B. The splittance of a graph.Combinatorica, 1981. Vol. 1. P. 275-284. DOI: 10.1007/BF02579333 EDN: NQRISL
6. Mahadev N. V. R., Peled U. N. Threshold Graphs and Related Topics. Ser. Annals of Discr. Math., vol. 56. Amsterdam: North-Holland Publ. Co., 1995. 542 p.
7. Merris R. Graph Theory. New York: J. Wiley & Sons Inc., 2001. 256 p. DOI: 10.1002/9781118033043
8. Merris R. Split graphs. European J.Combin., 2003. Vol. 24. P. 413-430. DOI: 10.1016/S0195-6698(03)00030-1 EDN: XPTWTV
9. Tyshkevich R. I. Decomposition of graphical sequences and unigraphs. Discrete Math., 2000. Vol. 220. P. 201-238. DOI: 10.1016/S0012-365X(99)00381-7 EDN: XKVSLV
Выпуск
Другие статьи выпуска
This paper addresses the time-optimal control problem of the Dubins car, which is closely related to the problem of constructing the shortest curve with bounded curvature between two points in a plane. This connection allows researchers to apply both geometric methods and control theory techniques during their investigations. It is established that the time-optimal control for the Dubins car is a piecewise constant function with no more than two switchings. This characteristic enables the categorization of all such controls into several types, facilitating the examination of the solutions to the control problem for each type individually. The paper derives explicit formulas for determining the switching times of the control signal. In each case, necessary and sufficient conditions for the existence of solutions are obtained. For certain control types, the uniqueness of optimal solutions is established. Additionally, the dependence of the movement time on the initial and terminal conditions is studied.
In this paper, the seminormed Cesàro difference sequence space ℓ(j, q, g, r,μ, Δ(s)t,) is defined by using the generalized Orlicz function. Some algebraic and topological properties of the space ℓ(j, q, g, r,μ, Δ(s)t,) are investigated. Various inclusion relations for this sequence space are also studied.
In this article, we establish a refined extension of the above integral inequality by using the polar derivative instead of the ordinary derivative consisting of the leading coefficient and the constant term of the polynomial. Besides, our result also yields other intriguing inequalities as special cases.
We calculate exact values of some n-widths of the class
For the class of bounded in l2-norm interpolated data, we consider a problem of interpolation on a finite interval [a, b] ⊂ ℝ with minimal value of the L2-norm of a differential operator applied to interpolants. Interpolation is performed at knots of an arbitrary N-point mesh ΔN: a ≤ x1 < x2 < < xN ≤ b. The extremal function is the interpolating natural -spline for an arbitrary fixed set of interpolated data. For some differential operators with constant real coefficients, it is proved that on the class of bounded in l2-norm interpolated data, the minimal value of the L2-norm of the differential operator on the interpolants is represented through the largest eigenvalue of the matrix of a certain quadratic form.
The paper analyzes average integral payoff indices for trajectories of the dynamic equilibrium and replicator dynamics in bimatrix coordination games. In such games, players receive large payoffs when choosing the same type of behavior. A special feature of a 2 × 2 coordination game is the presence of three static Nash equilibria. In the dynamic formulation, the trajectories of coordination games are estimated by the average integral payoffs for a wide range of models arising in economics and biology. In optimal control problems and dynamic games, average integral payoffs are used to synthesize guaranteed strategies, which are involved, among other things, in the constructions of the dynamic Nash equilibrium. In addition, average integral payoffs are a natural tool for assessing the quality of trajectories of replicator dynamics. In the paper, we compare values of average integral indices for trajectories of replicator dynamics and trajectories generated by guaranteed strategies in constructing the dynamic Nash equilibrium. An analysis is provided for trajectories of mixed dynamics when the first player plays a guaranteed strategy, and the behavior of replicator dynamics guides the second player.
In this paper, we prove certain Littlewood-Tauberian theorems for general matrix summability method by imposing the Tauberian conditions such as slow oscillation of usual as well as matrix generated sequence, and the De la Vallée Poussin means of real sequences. Moreover, we demonstrate (N, pn) and (C, 1) - summability methods as the generalizations of our proposed general matrix method and establish an equivalence relation connecting them. Finally, we draw several remarks in view of the generalizations of some existing well-known results based on our results.
The main aim of this paper is to present and explore some of properties of the concept of -statistical convergence in measure of complex uncertain sequences. Furthermore, we introduce the concept of -statistical Cauchy sequence in measure and study the relationships between different types of convergencies. We observe that, in complex uncertain space, every -statistically convergent sequence in measure is -statistically Cauchy sequence in measure, but the converse is not necessarily true.
Clustering is a strategy for discovering homogeneous clusters in heterogeneous data sets based on comparable structures or properties. The number of nodes or links that must fail for a network to be divided into two or more sub-networks is known as connectivity. In addition to being a metric of network dependability, connectivity also serves as an indicator of performance. The Euler graph can represent almost any issue involving a discrete arrangement of objects. It can be analyzed using the recent field of mathematics called graph theory. This paper discusses the properties of clustered networks like connectivity and chromaticity. Further, the structure of the antipodal graph in the clustered network has been explored.
The notion of f-statistical convergence in topological space, which is actually a statistical convergence’s generalization under the influence of unbounded modulus function is presented and explored in this paper. This provides as an intermediate between statistical and typical convergence. We also present many counterexamples to highlight the distinctions among several related topological features. Lastly, this paper is concerned with the notions of sf-limit point and sf-cluster point for a unbounded modulus function f.
We consider finite deterministic automata such that their alphabets consist of exactly one letter of defect 1 and a set of permutations of the state set. We study under which conditions such an automaton is completely reachable. We focus our attention on the case when the set of permutations generates a transitive imprimitive group.
The paper considers the problem of finding the reachable set for a linear system with determinate and stochastic Liu’s uncertainties. As Liu’s uncertainties, we use uniformly distributed ordinary uncertain values defined in some uncertain space and independent of one another. This fact means that the state vector of the system becomes infinite-dimensional. As determinate uncertainties, we consider feedback controls and unknown initial states. Besides, there is a constraint in the form of a sum of uncertain expectations. The initial estimation problem reduces to a determinate multi-step problem for matrices with a fixed constraint at the right end of the trajectory. This reduction requires some information on Liu’s theory. We give necessary and sufficient conditions for the finiteness of a target functional in the obtained determinate problem. We provide a numerical example of a two-dimensional two-step system.
In this study, beta Sturm-Liouville problems are discussed. For such equations, the spectral function is established in the singular case. A spectral expansion is given with the help of this function.
Статистика статьи
Статистика просмотров за 2025 - 2026 год.
Издательство
- Издательство
- УрФУ
- Регион
- Россия, Екатеринбург
- Почтовый адрес
- 620002, Свердловская область, г. Екатеринбург, ул. Мира, д. 19
- Юр. адрес
- 620002, Свердловская область, г. Екатеринбург, ул. Мира, д. 19
- ФИО
- Кокшаров Виктор Анатольевич (Ректор)
- E-mail адрес
- rector@urfu.ru
- Контактный телефон
- +7 (343) 3754507
- Сайт
- https://urfu.ru/ru